Below are the methodologies used by the World Bank to compile statistical data. They cover information from indicator definitions to aggregation rules and other World Bank processes in collecting data:

Data Consistency

Differences in timing and reporting practices may cause inconsistencies among data from different sources, so users should be cautious when combining these data.

Our comprehensive publications World Development Indicators and International Debt Statistics contain data that generally rely on official sources, although some adjustments are made in the balance of payments to account for fiscal/calendar-year differences. Within these publications we attempt to present data that are consistent in definition, timing and methods. Even so, updates and revisions over time may introduce discrepancies from one edition to the next.

National accounts and balance of payment data come from two sources: current reports gathered by the Bank's country management units and data obtained from official sources. The Country at a Glance tables may present data that differ from those reported in official sources.

Change in Terminology

Following statistical practice, the World Bank has adopted the following terminology in line with the 1993 System of National Accounts (SNA). The changes in terms are listed below.

Aggregation Rules

Aggregates are based on the World Bank’s regional and income classification of economies. Because of missing data, aggregates for groups of economies should be treated as approximations of unknown totals or average values. Regional and income group aggregates are based on the largest available set of data. The aggregation rules are intended to yield estimates for a consistent set of economies from one period to the next and for all indicators. Small differences between sums of subgroup aggregates and overall totals and averages may occur because of the approximations used. In addition, compilation errors and data reporting practices may cause discrepancies in theoretically identical aggregates such as world exports and world imports.

Five methods of aggregation are used in the World Development Indicators:

1. For group and world totals denoted in the tables by a t, missing data are imputed based on the relationship of the sum of available data to the total in the year of the previous estimate. The imputation process works forward and backward from 2010. Missing values in 2010 are imputed using one of several proxy variables for which complete data are available in that year. The imputed value is calculated so that it (or its proxy) bears the same relationship to the total of available data. Imputed values are usually not calculated if missing data account for more than a third of the total in the benchmark year. The variables used as proxies are GNI in U.S. dollars, total population, exports and imports of goods and services in U.S. dollars, and value added in agriculture, industry, manufacturing, and services in U.S. dollars.
2. Aggregates marked by an s are sums of available data. Missing values are not imputed. Sums are not computed if more than a third of the observations in the series or a proxy for the series are missing in a given year.
3. Aggregates of ratios are generally calculated as weighted averages of the ratios (indicated by w) using the value of the denominator or, in some cases, another indicator as a weight. The aggregate ratios are based on available data, including data for economies not shown in the main tables. Missing values are assumed to have the same average value as the available data. No aggregate is calculated if missing data account for more than a third of the value of weights in the benchmark year. In a few cases the aggregate ratio may be computed as the ratio of group totals after imputing values for missing data according to the above rules for computing totals.
4. Aggregate growth rates are generally calculated as a weighted average of growth rates (and indicated by a w). In a few cases growth rates may be computed from time series of group totals. Growth rates are not calculated if more than half the observations in a period are missing. For further discussion of methods of computing growth rates see below.
5. Aggregates denoted by an m are medians of the values shown in the table. No value is shown if more than half the observations for countries with a population of more than 1 million are missing. Exceptions to the rules occur throughout the book. Depending on the judgment of World Bank analysts, the aggregates may be based on as little as 50 percent of the available data. In other cases, where missing or excluded values are judged to be small or irrelevant, aggregates are based only on the data shown in the tables.

Growth Rates

Growth rates are calculated as annual averages and represented as percentages. Except where noted, growth rates of values are computed from constant price series. Three principal methods are used to calculate growth rates: least squares, exponential endpoint, and geometric endpoint. Rates of change from one period to the next are calculated as proportional changes from the earlier period:

Least-squares growth rate. Least-squares growth rates are used wherever there is a sufficiently long time series to permit a reliable calculation. No growth rate is calculated if more than half the observations in a period are missing. The least-squares growth rate, r, is estimated by fitting a linear regression trend line to the logarithmic annual values of the variable in the relevant period. The regression equation takes the form:

which is equivalent to the logarithmic transformation of the compound growth equation,

In this equation X is the variable, t is time, and a = ln Xo and b = ln (1 + r) are parameters to be estimated. If b** is the least-squares estimate of *b, the average annual growth rate, r, is obtained as [exp(*b**) – 1] and is multiplied by 100 for expression as a percentage.

The calculated growth rate is an average rate that is representative of the available observations over the entire period. It does not necessarily match the actual growth rate between any two periods.

Exponential growth rate. The growth rate between two points in time for certain demographic indicators, notably labor force and population, is calculated from the equation

                                                                                                  

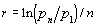
in the period, and ln is the natural logarithm operator. This growth rate is based on a model of continuous, exponential growth between two points in time. It does not take into account the intermediate values of the series. Nor does it correspond to the annual rate of change measured at a one-year interval, which is given by (pn – pn-1)/pn-1.

Geometric growth rate. The geometric growth rate is applicable to compound growth over discrete periods, such as the payment and reinvestment of interest or dividends. Although continuous growth, as modeled by the exponential growth rate, may be more realistic, most economic phenomena are measured only at intervals, in which case the compound growth model is appropriate. The average growth rate over *n8 periods is calculated as

                                                                                           

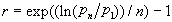
Like the exponential growth rate, it does not take into account intermediate values of the series.

World Bank Atlas Method

The Atlas conversion factor for any year is the average of a country’s exchange rate (or alternative conversion factor) for that year and its exchange rates for the two preceding years, adjusted for the difference between the rate of inflation in the country, and a group of countries. From 2016 onwards, these countries include the Euro Zone, China, Japan, the United Kingdom and the United States. A country’s inflation rate is measured by the change in its GDP deflator. The international inflation rate is measured by the change in the SDR deflator (Special drawing rights, or SDRs, are the IMF’s unit of account). The SDR deflator is calculated as a weighted average for a group of countries’ (since 2016 the Euro Zone, China, Japan, the United Kingdom, and the United States) GDP deflators in SDR terms, the weights being the amount of each country’s currency in one SDR unit. Weights vary over time because both the composition of the SDR and the relative exchange rates for each currency change. The SDR deflator is calculated in SDR terms first and then converted to U.S. dollars using the SDR to dollar Atlas conversion factor. The Atlas conversion factor is then applied to a country’s GNI. The resulting GNI in U.S. dollars is divided by the midyear population to derive GNI per capita. When official exchange rates are deemed to be unreliable or unrepresentative of the effective exchange rate during a period, an alternative estimate of the exchange rate is used in the Atlas formula (see below). The following formulas describe the calculation of the Atlas conversion factor for year t:

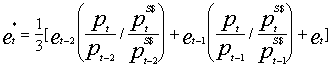
and the calculation of GNI per capita in U.S. dollars for year t :

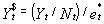
where et* is the Atlas conversion factor (national currency to the U.S. dollar) for year t, et is the average annual exchange rate (national currency to the U.S. dollar) for year t, pt is the GDP deflator for year t, pt S$ is the SDR deflator in U.S. dollar terms for year t, Yt $ is the Atlas GNI per capita in U.S. dollars in year t, Yt is current GNI (local currency) for year t, and Nt is the midyear population for year t.

Alternative Conversion Factors

The World Bank systematically assesses the appropriateness of official exchange rates as conversion factors. An alternative conversion factor is used when the official exchange rate is judged to diverge by an exceptionally large margin from the rate effectively applied to domestic transactions of foreign currencies and traded products. This applies to only a small number of countries. Alternative conversion factors are used in the Atlas methodology and elsewhere in the World Development Indicators as single-year conversion factors.